The following complete article may be found under :
C. J. Ballhausen, Quantum Mechanics
and Chemical Bonding in Inorganic Complexes.
J. Chem. Ed. 56, 294-297 (1979).
Please note : This page does need the type font "Symbol" (Greek).
Quantum Mechanics and Chemical Bonding
in Inorganic Complexes. II.
C. J. Ballhausen
University of Copenhagen,
Copenhagen, Denmark
II. Valency and Inorganic Metal Complexes.
The Valence Bond Method
In his book published in 1927 Sidgwick summed up the
electronic interpretation of coordination as follows
In the first place it is clear that the links which join the units of a
coordination complex to the central atom are covalent. This is really
self-evident if our theory is true, since Werner showed that they were
not ionized, and a covalent link is the only alternative which we have
admitted; but it is established conclusively by the final tests of
geometrical and optical isomerism. Hence the maximum coordination
number is the maximum covalency number: an atom with a coordination
number of six is one which can form six covalencies, and so have
a valency group of twelve shared electrons.
The working out of these ideas in a quantum mechanical
language was done by Pauling (27). In his very important
paper of 1931 he showed
that many more results of chemical significance can be obtained from
the quantum mechanical equations, permitting the formulation of
an extensive and powerful set of rules for the electron-pair bond
supplementing those of Lewis.
We shall here concentrate on Pauling's work on the
transition metal coordination compounds (27, 28). The basic
problem to solve was which metal orbitals should be used to
form the Heitler-London covalent bonds with the ligands.
Pauling showed that by using a single 3d eigenfunction, the
4s and two 4p eigenfunctions, four equivalent strong bonds
can be formed, and these lie in a plane, directed toward the
corners of a square. Using a
(3d)2(4s)1(4p)3 hybridization, six
equivalent eigenfunctions can be formed directed toward the
corners of a regular octahedron. A (3d)3(4s)1 hybridization
would lead to four equivalent strong bonds directed toward
the corners of a tetrahedron. These hybrid orbitals could then
be used in the formation of covalent electron pair bonds. The
electrons which formed the bonds were supplied from lone
pairs of electrons on the ligands.
The numbers and types of metal orbitals which had to be
used in the construction of the
sp2d (square planar) sp3d2
(octahedral) and sd3 (tetrahedral) hybrids appeared to be
something of a mystery. Using group theory this was, however,
cleared up by Van Vleck (29)
in 1935. Concentrating on what
we now call s-bonding (sigma ~)
between the metal atom and the ligands
Van Vleck showed that for the
directional properties... to be correlated with one particular attached
atom ... the Pauling-Slater central functions must have the same
transformation properties as do those wave-functions of the attached
atoms before linear combinations of the latter are taken.
An example (29) may clarify this. Using the modern lan-
guage of group theory, the six ligänd sigma bonds in an
octahedrally coordinated metal complex span the irreducible
representations a1g, eg and t1u.
The metal orbitals span
(s) : a 1g,
(p x, p y, p z) : t 1u,
(d 3z 2 - r 2 ,
d x 2 - y 2) : t 2g
and (dxy, d xz, d yz ) : t 2u.
By comparison we see that the d t 2g orbitals are entirely
sigma non-bonding. In this way, the metal d-orbitals which form
octahedral hybrids are seen to be
d x 2 - y 2 and
d 3 z 2 - r 2.
A quantum mechanical calculation of the 12-electron
valence bond wave function which can be written down for an
octahedral complex was at that time an impossible undertaking.
Pauling's bonding scheme remained therefore a
postulate, unsupported by numerical calculations. However,
modern molecular orbital calculations have shown that the
picture is essentially correct. The greatest element of weakness
in Pauling's bonding theory was pointed out by Van Vleck and
Sherman (26), namely that ligand electrons to a large extent
had to be absorbed by the central metal ion. For instance, for
an octahedral complex six ligand electrons had to be
transferred to the central atom. Many years later Pauling took
account of this critique and formulated (30) the
postulate of the essential electrical neutrality of atoms: namely, that
the electronic structure of substances is such as to cause each atom
to have essentially zero resultant electric charge.
In an octahedral complex [M 3+ L 6]
this couId be achieved with
the use of only three metal orbitals, resonating among the six
positions. Each bond therefore would be 50% ionic and 50%
covalent. A true valence bond wave function is of course a
linear combination of functions representing the different
possible phases through which the system resonates. Yet
again, it must be said that the numerical testing of Pauling's
ideas was out of the question.
Assuming a saturated valence bond scheme the next
question which had to be answered was where to accommodate the
surplus metal electrons. In his 1931 paper Pauling makes a
distinction between. "an electron-pair bond structure" and an
"ionic structure". In an electron-pair bond scheme for an
octahedral metal complex three 3d orbitals (the t 2g orbitals) are
empty, and thus can be used to house the metal electrons.
However, when more than six metal electrons were present
more orbitals were needed. Either the electrons had to occupy
the two 3d (e g) orbitals, which therefore could not be used for
bonding purposes, or they had to be accommodated in the
high-lying 4d orbitals. The last situation was thought to lead
to very unstable complexes. Consequently the problem of
where to house the "surplus" electrons could be met only by
assuming an "ionic structure" for the complex. As to the actual
type of bonding utilized in the complexes Pauling suggested
that in many cases this could be inferred from a knowledge of
the magnetic moments of the complexes.
Let L and S be the quantum numbers corresponding to the
total angular orbital momentum and the total Spin momentum
of the electrons. Provided the interaction between L and S is
small, so that the multiplet separation is small compared with
kT, the magnetic moment of an atom is given by Van Vleck's
formula (39)
m =
SQR [ 4 S ( S + 1) + L ( L + 1)]
{SQR=square root}
Pauling now reaches the conclusion that
the perturbing effect of the atoms or molecules surrounding a
magnetic atom destroys the contribution of the total momentum to the
magnetic moment, ... the magnetic moment of a molecule or complex
ion is determined entirely by the number of unpaired electrons, being
equal to
m = 2 SQR [ S ( S + 1 ) ].
Using this criterion he observed, for instance, that the
complex
Fe(H2O) 6 2 +
with six 3d electrons had a magnetic
moment of 5.25, corresponding roughly to S =2.
Fe(CN) 6 4 - on
the other hand had S = 0. Hence the bonding in
Fe(H2O) 6 2 +
was "ionic" but in
Fe(CN) 6 4 - on
it was "covalent".
Boldly, Pauling
further used measurements of magnetic susceptibilities to
infer molecular structures. The
Ni(CN)4 2 -
complex is diamagnetic, and provided we use one 3d orbital to form four
square planar covalent bonds, the eight metal electrons can
only be housed in the remaining four 3d orbitals, all being
paired up in the spins. From this Pauling predicted that the
Ni(CN)4 2 -
complex should be planar. No X-ray data on this
ion were available when Pauling made his prediction, but the
fact was soon established.
With very little effort and with virtually no knowledge of
theory it was therefore possible for inorganic chemists to make
magnetic measurements and to classify complexes as "ionic"
or "covalent." Many molecular structures were further
predicted on the basis of susceptibility measurements. Most of
this work has been shown by time to be unreliable. As we shall
see next Van Vleck soon proved that the "magnetic criterion"
was not of much value, and Pauling also realized this later (30).
In 1948 he said
We conclude accordingly that the magnetic criterion distinguishes,
not between essentially covalent bonds and essentially ionic bonds,
but between strong covalent bonds, using good hybrid bond orbitals
and with the possibilities of unsynchronized ionic-covalent resonance,
and weak covalent bonds, using poor bond orbitals, and with the
necessity for synchronization of the covalent phases of the bonds. In a
complex of the first sort the stability of the complex is due in larger
part to the bond themselves and in smaller part to the atomic
electrons, and in a complex of the second sort the situation
is reversed.
In his 1948 statement Pauling tried to conceal by a
circumlocution that his original simple theory was unable to deal
with the accumulated experimental evidence. The history of
chemistry has taught us that whenever a theory cannot put
numbers to its findings, but shrouds itself in a verbal mist, it
is time to abandon it. Let us, however, also reflect for a minute
that in 1931 Pauling gave a basically correct explanation of
the bonding in organic transition metal complexes and also
gave an accurate description of the electronic configurations
of the ground states in those complexes where one only needs
to include the 3d (t 2g) atomic orbitals. Had Pauling also as a
matter of course utilized the two 4d (e g) orbitals as recipients
for the metal electrons, and used the energy separation
between the 3d (t2g) and 4d (e g)
orbitals as a parameter, the
history of transition metal chemistry would undoubtedly have
been advanced many years. Evidently Pauling had not read
the two-year-old paper by Bethe (16);
had he done so, the idea
should have been obvious. lt would have provided the natural
explanation of the variations in the magnetic moments of the
complexions without any ad hoc explanations. However,
notwithstanding all "bonding theories" the time was evidently
not ripe to realize that the complexes are just not thinly
disguised metal ions, but true molecular entities.
The Crystal Field and Magnetic Susceptibilities
Using "the new quantum mechanics" the formulas for the
magnetic susceptibility of a molecule had been worked out by
Van Vleck (31) in 1928. A new result was obtained from these,
namely that molecules without a spin may still be slightly
paramagnetic. In addition to the usual diamagnetic term
proportional to
- S i « r i 2»,
{website notice :
the <> are not possible under HTML and are replaced by : « » }
there is also for a molecule a positive, so-called, high frequency term.
It is also called the Van
Vleck term after its discoverer. The reason for its presence is
that for a molecule
« n| L|n » may be zero but « n| L 2|n » never
is. The sum of the diamagnetic term and the high frequency
term is invariant of which point we take as the origin of r i.
The cases of most interest are, however, those where the
molecules possess spin magnetism. The work of Bethe (16)
had advanced the model based on the idea that in a complex
the electrons associated with the central atom experience an
electric field coming from the surrounding ligands. The year
1932 saw Van Vleck and his coworkers busily engaged in
investigating how the "crystal field" of the ligands would
influence the paramagnetic susceptibility of the central
transition metal ion.
Van Vleck wrote (32)
I was away from Madison for most of 1930 because I was in Europe
on a Guggenheim Fellowship.... Near the beginning of my fellowship
(I had) a walk with Kramers along some of the dunes in Holland. He
told me of Bethe's wonderful group theory paper on the energy levels
of magnetic ions in crystals, and also of his own work on the double
degeneracy of odd ions. I feel I learned more in this one walk than in
the whole rest of my fellowship. One can never tell when a turning
point will arise in one's career in research .... When I returned to
Wisconsin... I was kept busy finishing up my book on Electric and
Magnetic Susceptibilities, as well as learning group theory so I would
have a thorough understanding of Bethe's paper. However, in the late
summer of 1931, two physicists from Great Britain came to Madison
on post-doctoral fellowships, William (now Lord) Penney, and Robert
Schlapp, and I suggested that they work respectively on the effect of
a crystalline field on the paramagnetic susceptibilities of rare earth
compounds and of salts containing certain ions of the iron group.
Let us consider the second paper by Schlapp and Penney
(33), "Influence of Crystalline Fields on the Susceptibilities
of Salts of Paramagnetic Ions... ‚ especially Ni, Cr and Co".
As their starting point they took the well known spectroscopic
term for the ground states of
Ni 2+ ( 3 F) ,
Cr 3+ ( 4 F) , and
Co 2+ ( 3 F).
The electric field of the crystal is then able to break down
the relatively weak coupling between orbit and spin, and the
spin-orbit coupling may be treated as a perturbation on an
unperturbed problem which neglects the spin. The
unperturbed problem is then the same for all the above three ions,
since they all have an F state as ground state. Notice that the
troublesome 1/r 12 terms, which in all other molecular
problems are a great bottle-neck, in this model are already
incorporated in the zero-order functions.
The crystalline potential in salts of the iron group is
dominantly cubic, corresponding to a regular octahedral six-fold
coordination of the metal ions. For d-electrons the most
general crystalline potential with cubic symmetry was shown
by Van Vleck (34) to be
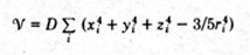
For Ni 2+ and Cr 3+
such a cubic field will split the F state
leaving a one-fold orbital degenerate state of A 2g symmetry
as the ground state provided D is positive, but in octahedral
Co2+ complexes it will be a three-fold orbital degenerate
T 1g
state. Now a T 1g state is also susceptible to spin-orbit
coupling. It can carry orbital momentum and it can split into
further components in a lower than cubic crystai field. None
of these effects are operative in a A 2g state. The first triumph
of crystal field theory was therefore that it explained why
nickel salts are nearly isotropic magnetically, while those of
Co 2+ exhibit large anisotropies even though the
Ni 2+ and Co 2+
ions are both in F states and are adjacent in the periodic table.
As stated by Van Vleck (32)
The article [34] in which I published this result is my favorite of the
various papers I've written as it involved only rather simple calculations,
and yet it gave consistency and rationality to the apparently
irregular variations in magnetic behaviour from ion to ion.... In fact
I still have some reprints left of my favorite 1932 paper. In the postwar
era its results are considered well known, and the calculation
straight forward — hence no need of a reprint.
Provided the orbital contribution to the magnetic moment
is neglected, the magnet on number would be the spin-only
value 2 SQR [ S ( S + 1) ]. A one-fold orbital degenerate state cannot,
in first order, carry any orbital momentum. However, the
spin-orbit coupling may give rise to an orbital contribution
to the magnetic moment of a one-fold degenerate state.
The spin magnetic moment of an electron in measured in
Bohr magnetons, b.
The ratio of the magnetic moment to the
angular momentum in two times as great for the spin as for the
orbital motion. The total angular momentum J of an atom is
a constant; it is made up of orbital, L, and spin, S,
contributions from the electrons. Therefore
J = L + S. The magnetic
moment,
b ( L + 2 S ),
will not in general be a constant, but will
in each state have an average value. This will be equal to its
projection on the constant total angular momentum. The
ratio, g, of the projection of the magnetic moment on the
angular momentum to the angular momentum is thus
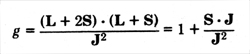
From J - S = L do we
get 2 J dot S = J 2 + S
2 - L 2.
With J 2 , L 2 ,
and S 2 being diagonal with values J ( J + 1 ), L ( L + 1 ) and
S ( S + 1 ) we have for the Landé g factor
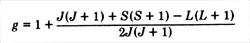
With L = 0, we have g = 2, the spin-only value.
Let the crystal field perturbation Hamiltonian be
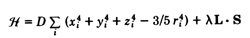
Here l is the spin-orbit coupling constant.
l is positive in the
first half of an atomic shell, negative in the last half. The
orbital contribution to a one-fold degenerate state will therefore
by second order perturbation theory be given as the expectation
value « L » ~= l / D.
Identifying L with « L », we see how
Schlapp and Penney could explain why the deviations of the
effective Lande g factor should be positive for the ( 3d ) 8 system
of Ni 2+ and negative for the ( 3d ) 3
system of Cr 3+. Fitting their
formulas for the magnetic susceptibilities to the available
experimental data they found 10 Dq = 12600 cm -1 for
Ni(H2O)6 2+ and 10 Dq = 37,300 cm -1 for
Cr(H 2O) 6 3+. The
"modern" spectroscopic values are 8500 -1 and 17,400
cm -1, respectively. Particularly the Cr 3+ value is
therefore off by more than a factor of two.
By doing an electrostatic calculation Gorter (35) had shown
that provided D is positive for an octahedral arrangement of
six ligands, it will be negative for a tetrahedral four
coordination. This had importance for the work of Jordahl (36) on
the magnetic susceptibility of CuSO4 - 5H20. In 1933 it was
generally supposed that the Cu2+ ion was four-coordinated.
The magnetic susceptibility of CuSO4 - 5H20 could, however,
only be explained by Jordahl on the assumption of a positive
D. The agreement between the calculated and observed mean
susceptibility was therefore taken as an indication of an
octahedral arrangement around the Cu2+ ion. The X-ray proof
that this was indeed so was given very shortly after (37).
For an orbital degenerate ground state one should not a
priori expect a "spin-only" formula for the magnetic
susceptibility to be valid. As the measurements of magnetic
susceptibilities as a function of temperature accumulated it
became, however, apparent that the "spin-only" formula had
a much wider applicability than expected. In cases where a
cubic crystal field would lead to orbital degeneracies it was,
therefore, necessary to include crystal fields of lower
symmetry than cubic in order to do away with the orbital
degeneracies.
A hexacoordinated magnetic ion of course need not be
located in the crystal at a point having cubic symmetry. Such
a situation would naturally introduce lower than cubic
elements in the field. However, as first pointed out by Van Vleck
(38) in 1939, the Jahn-Teller effect will always see that the
arrangement of the ligands is such that all orbital degeneracy
is abolished.
The Jahn-Teller effect! How many times since its discovery
in 1937 has this theorem (39) (which is not an effect at all) not
been invoked to explain troublesome molecular electronic
manifestations. As to its discovery Edward Teller records
(40):
In the year 1934 both Landau and I were in the Institute of Niels Bohr
at Copenhagen. We had many discussions. I told Landau of the work
of one of my students, R. Renner, on degenerate electronic states in
the linear CO2 molecule ... (Landau) said that I should be very
careful. In a degenerate electronic state the symmetry on which the
degeneracy is based will in general be destroyed. I managed to
convince Landau that his doubts were unfounded (for a linear molecule).
A year later in London I asked myself the question whether another
exception to Landau's postulated statement might exist ....
The question did not appear simple. I proceeded to discuss the
problem with H. A. Jahn who, as I, was a refugee from a German
university. We went through all possible symmetries and found that
linear molecules constitute the only exception. In all other cases
Landau's suspicion was verified.
Jahn (41) extended the theorem to cover the cases where
there is both spin and orbital degeneracy. A non-linear
symmetrical position of a polyatomic molecule cannot be stable
if there is other spin degeneracy than a Kramers spin doublet.
The spin-orbit coupling can consequently stabilize a nonlinear
configuration which would be unstable if orbital
degeneracy alone were present, provided the coupling is large
and leaves as its lowest state a non-degenerate "double group"
state or a Kramers doublet.
Jahn and Teller (39) showed that orbital electronic
degeneracy and stability of the nuclear configuration are
incompatible unless all the atoms of the molecule lie on a
straight line. Their proof was based on group theory and it
does not give any recipe as to how to calculate the magnitude
of the instability. The simplest molecular system which should
exhibit a Jahn-Teller configurational instability is the
equilateral triangle configuration of H3. For this three-electron
system it was already possible in 1938 for Hirschfelder (42)
to calculate the angle dependence of the energy by the
variational method. lt was found that the (unstable) H3 system had
its lowest energy for a linear configuration.
The Jahn-Teller instability of the big octahedral complexes
had, however, to be attacked by perturbation methods. The
necessary mathematical theory was worked out by Van Vleck
(43) and a calculation made of the magnitude of the effect. As
his perturbation Hamiltonian Van Vleck took an expansion
of the crystal field potential in the octahedral vibrational
symmetry coordinates
e g and
t 2g. To this he added a
permanent trigonal field
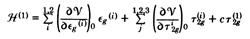
For an E state, only the first term in active; the locus of
minimum energy in a circle in the
e g ( 1 ) ,
e g ( 2 ) plane.
This in the, by now
well known, "Mexican hat" potential surface. For T1 and T2
states, it was found that with the first term in
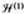 being
dominant we would have a tetragonal distortion; with a
dominans of the last two terms the distortion would be along
a body diagonal of the octahedron. For instance, for
Ti(H 2O) 6 3+
with a ground state of 2 T 2 the tetragonal
splitting of T2 was
calculated to be 315 cm -1, the trigonal splitting to be 550
cm -1.
being
dominant we would have a tetragonal distortion; with a
dominans of the last two terms the distortion would be along
a body diagonal of the octahedron. For instance, for
Ti(H 2O) 6 3+
with a ground state of 2 T 2 the tetragonal
splitting of T2 was
calculated to be 315 cm -1, the trigonal splitting to be 550
cm -1.
The treatment Van Vleck gave the Jahn-Teller configurational
instability problem of octahedral complexes is by now
the standard procedure. In 1939 it must have been a tour de
force. Its significance was not understood until long after the
war.
Literature Cited
(27) Pauling, L., J. Amer. Chem. Soc., 53, 1367 (1931).
(28) Pauling, L., J. Amer. Chem. Soc., 54, 988 (1932).
(29) Van Vleck, J. H., J. Chem. Phys., 3, 803 (1935).
(30) Pauling, L., J. Chem. Soc., 1461 (1948).
(31) Van Vleck, J. H., Phys, Rev., 31, 587 (1928).
(32) Van Vleck, J. H., Int. J. Quantum Chem. Symp., 5, 3 (1971).
(33) Schlapp, R., and Penney, W. G., Phys. Rev., 42, 666 (1932).
(34) Van Vleck, J. H., Phys. Rev., 41, 208 (1932).
(35) Gorter, C. J., Phys. Rev., 42, 437 (1932).
(36) Jordahl, 0. M., Phys. Rev., 45, 87 (1934).
(37) Beevers, C. A., and Lipson, L.,
Proc. Roy. Soc. (London) A146, 570 (1934).
(38) Van Vleck, J. H., J. Chem. Phys., 7, 61(1939).
(39) Jahn, H. A., and Teller, E.,
Proc. Roy. Soc. (London), A161, 220 (1937).
(40) Englman, R., "The Jahn.Teller Effect in Molecules and Crystals.
An Historical Note,
Wiley.Interscience, New York, 1972.
(41) Jahn, H. A., Proc. Roy. Soc. (London), A164, 117 (1938).
(42) Hirschfelder, J. 0., J. Chem. Phys., 6, 795 (1938).
(43) Van Vleck, J. H., J. Chem. Phys., 7, 72 (1939).
Goto:
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. I.
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. II. = this page here, go top
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. III.
Last updated : Apr. 23, 2002 - 19:47 CET




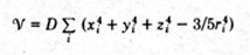
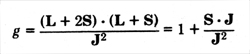
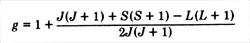
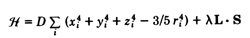
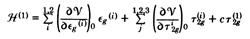
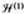 being
dominant we would have a tetragonal distortion; with a
dominans of the last two terms the distortion would be along
a body diagonal of the octahedron. For instance, for
Ti(H 2O) 6 3+
with a ground state of 2 T 2 the tetragonal
splitting of T2 was
calculated to be 315 cm -1, the trigonal splitting to be 550
cm -1.
being
dominant we would have a tetragonal distortion; with a
dominans of the last two terms the distortion would be along
a body diagonal of the octahedron. For instance, for
Ti(H 2O) 6 3+
with a ground state of 2 T 2 the tetragonal
splitting of T2 was
calculated to be 315 cm -1, the trigonal splitting to be 550
cm -1.